土抗剪强度是设计地基结构时最基本的性质,应仔细评估和了解。介绍了几种预测非饱和土抗剪强度的经验模型。然而,这些预测模型的适用性和敏感性存在不确定性。本文对现有理论模型的信度和效度进行了全面的验证研究。利用30个实验数据集,将预测模型得到的结果与实测数据进行了比较。还进行了性能分类程序,以评估分析模型对不同土壤类型以及大范围的基质吸力、饱和度、土壤密度、土壤塑性和粘土活性的适用性。微观结构研究阐明了各单一参数的影响,也为非饱和土的力学研究提供了新的思路。结果表明,模型对砂质土的适用性较好,对粘性土的适用性较差。抗剪强度模型的性能随基质吸力、初始密度、塑性指数和粘土活性的增加而降低。因此,建议根据土的类型和性质仔细选择抗剪强度估计模型。此外,分析结果还指出,将Bishop方程中的因子\(\chi\)设为饱和度的选择只适用于基质吸力较低的中致密土。这种假设对粘性土或具有高基质吸力的致密土尤其无效。
为了设计工程结构,抗剪强度是土的最基本的特性,应该正确地评估和理解。浅基础、挡土墙、开挖、桩基础、边坡稳定性、侵蚀风险预测以及其他涉及土-结构相互作用的岩土工程应用的能力是使用土抗剪强度的岩土工程应用的几个例子(Yao and Yang 2017;Fattah et al. 2020;Nouzari et al. 2021;Zhang et al. 2021;范教授2022年;Pham et al. 2022;Pham and Sutman 2023a)。确定非饱和土的抗剪强度并能够量化可能由于环境条件而发生的抗剪强度变化是很重要的(Xu 2004;Dong et al. 2015;Mun et al. 2018;Yang et al. 2019;范和苏特曼2022a;Alassal et al. 2023;Pham et al. 2023a)。此外,由于去饱和是液化的潜在对策,非饱和土抗剪强度已被认为是液化研究中的一个重要因素(Mele and Flora 2019;Mele et al. 2022)。然而,非饱和抗剪强度测量具有挑战性、昂贵且耗时长。因此,理论预测成为一种至关重要的方法,特别是在初步设计阶段以及数值模拟(Honda et al. 2011;盛等,2011;范教授2020年;Pham等。2021,2023b;Chali and Maleki 2021)。
提出了几种描述非饱和土抗剪强度的经验模型,它们都是基于有效应力的理论框架。土性函数建立了抗剪强度与基质吸力之间的联系,是现有估计模型之间的主要区别。提出了几种不同类型的土壤性质函数,如使用饱和度(?berg和S?llfors 1997;Zhou et al. 2018;Zhai et al. 2019),体积含水量(Lamborn 1986;Aubeny和Lytton 2003),体积空气含量(Graecen 1960),标准化含水量(Vanapalli et al. 1996;Fredlund et al. 1996;塔伦蒂诺和汤博拉托2005;Oh and Vanapalli 2014),以及空气进入值(Khalili and Khabbaz 1998;Lee et al. 2005;Kayadelen et al. 2007;Satyanaga和Rahardjo 2019)。文献综述也表明,许多现有的抗剪强度模型在形式上是线性的。然而,吸力和抗剪强度之间的关系可能是非线性的,这取决于土壤类型或吸力值的范围(Karube和Kawai 2001;盛等,2011;Jiang et al. 2020;Pham and Sutman 2022b)。
需要注意的是,孔隙度、容重、应力状态、含水量、化学成分、土壤结构等多种土壤和环境特征对非饱和抗剪强度都有影响。由于土壤的复杂性质和环境条件的变化,在实践中产生了许多不同的场景。因此,寻找一种可靠的非饱和抗剪强度估算模型的需求日益增加。不幸的是,几乎所有的经验模型都是使用有限数量的数据集建立和验证的。此外,它们的适用性经常在低吸力范围内得到验证,但它们并没有证明如何应用这些方程来预测高吸力(如残余区)的非饱和土的抗剪强度。因此,不可能建立一个特定的模型,能够准确地预测所遇到的每种土壤在大吸力范围内的非饱和抗剪强度。因此,总是需要在广泛的土壤条件下使用独立的实验数据集来验证抗剪强度模型(Marinho和do Amaral Vargas Jr 2020)。
在其他方面,随着岩土工程师越来越意识到非饱和土壤经验模型带来的不确定性,他们开始朝着更合理的基于可靠性的设计方向发展(Sillers and Fredlund 2001;Bozorgzadeh et al. 2019;Ching et al. 2021;郭等,2022;郭等,2023;Pham et al. 2023c)。为了说服岩土工程师在日常实践中应用非饱和土力学理论,评估使用统计分析方法可以断言的分析模型的准确性是重要的。本文中发现的不确定性将作为一个基准来决定哪些模型适合于各种类型的土壤。
本文有以下四个主要目标。(1)利用30个不同的试验数据集对现有的抗剪强度模型进行了全面的验证研究。每种抗剪强度模型的优缺点都与统计评估有关。(2)评价不同分析模型的相对适宜性及其对非饱和土的适用性。(3)提供一个性能分类程序,为选择模型可靠地估计各种土壤条件下非饱和土的抗剪强度提供基础。(4)讨论高吸力或大吸力范围下各种抗剪强度方程的有效性。
文献中提出了许多模型来预测非饱和土的抗剪强度。然而,对所有可用的抗剪强度模型进行验证是很困难的。因此,在选择抗剪强度模型进行对比时,提出以下准则:(i)所选模型不应包含任何拟合参数,(ii)抗剪强度模型应以Bishop应力法或Fredlund独立应力法的形式制定,(iii)所选模型应在报告、设计指南、标准中得到推荐,或应在实践中以预测而知名,(iv)所选抗剪强度模型应包括不同的土壤性质函数。基于上述四个准则,本研究选取了7种知名的抗剪强度模型进行对比。下面简要介绍所选抗剪强度模型的特点。
应力张量的法向分量和剪切分量通过抗剪强度本构关系在数学上联系起来。扩展有效应力理论和Mohr-Coulomb破坏准则来描述非饱和土的抗剪强度是大多数现有方程的共同特征(Pham 2022b)。
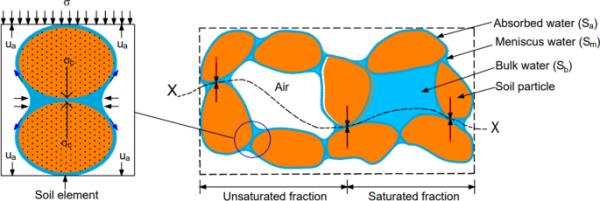
考虑如图1所示的两粒非饱和土的接触。两粒间的载荷传递部分通过粒间接触压力(Pc)、孔隙水压力(Pw=Pw1 + Pw2)和孔隙空气压力(Pa=Pa1 + Pa2)来实现。对于非饱和土,力的平衡得到下式:
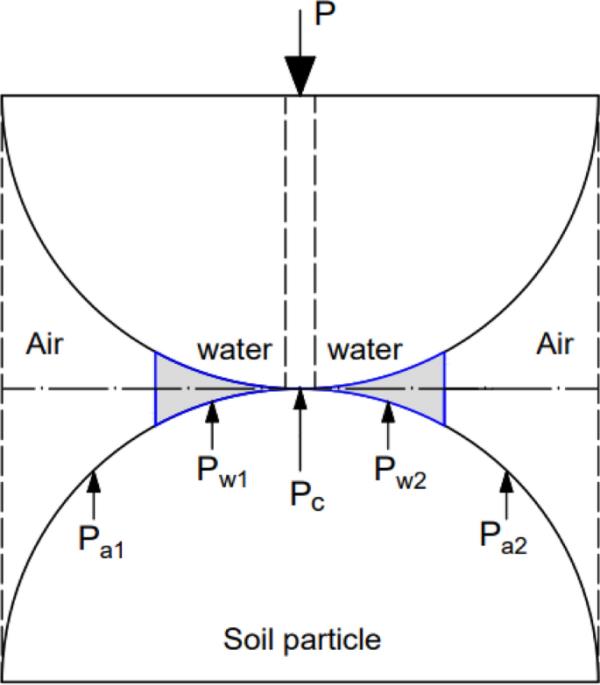
微机械应力分析模型
(1)在应力平衡下,式(1)也可以改写为:
(2)将整个式(2)除以总横截面积得到
(3)或者,
(4)式中=总法向应力,=接触应力,=有效应力或等效应力,=孔隙-空气压力,=孔隙-水压力,=水面积,=颗粒接触面积,A=总横截面面积。
谷物接触比例(通常被认为可以忽略不计,可以忽略不计。采用Mohr-Coulomb破坏准则可将非饱和土抗剪强度一般方程转化为:
(5)式中τ=非饱和抗剪强度,(σ -)=净法向应力,(-)=ψ=基质吸力,=有效摩擦角,c'=有效黏聚力。
如果=χ, Eq.(5)表示为:
(6)有时被称为毕晓普参数。完全饱和土的值为,而干燥土的值为。结果表明,该数值主要取决于饱和水平、土体结构和应力状态。需要强调的是,现有抗剪强度模型之间的主要区别在于归一化水函数(或Bishop参数)的定义。
根据毛细模型,上式中的基质吸力项表示孔隙空气压力和孔隙水压力由于表面张力的差异。然而,基质吸力值的变化并不直接对应于中性应力的变化,因为它代表了由于张力表面通常仅作用于土壤颗粒表面积的一部分而产生的压力差。的值的显著变化通常伴随着基质吸力的变化。此外,样品中土壤结构的变化是由土壤中存在的强表面张力引起的,这已被证明对体积变化特别重要。
Greacen(1960)利用环剪仪对高孔隙率(孔隙比为1.2)的塑性粘土进行了试验,研究吸力对土体抗剪性能的影响。可以看出,在低法向压力下(图2中的OA),抗剪强度与施加荷载呈线性关系。然而,当荷载足够强,将土压缩至饱和时,这种关系就变得高度非线性,塑性粘土的AD曲线就是如此。在此基础上,提出了吸力作为内部接触面积的附加荷载,增加了土的抗剪强度。考虑吸力对非饱和土抗剪强度增加的影响,通过分数充气空隙来考虑,其如下:
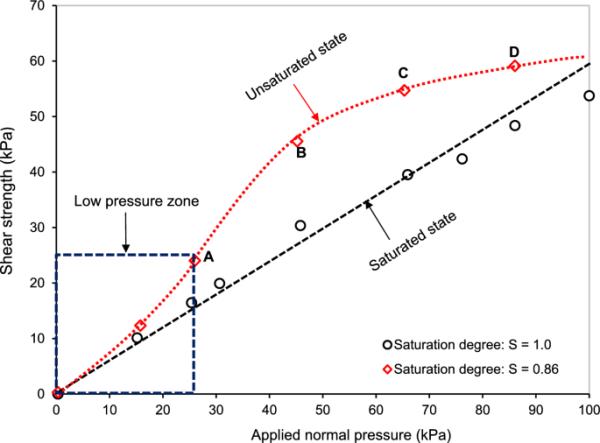
塑性粘土抗常压最大抗剪强度(数据自Greacen 1960年以后)
(7) (8)Greacen(1960)对抗剪强度方程的表达式为:
(9)式中=孔隙度,=体积空气含量,=体积含水量。
Lamborn(1986)提出了基于细观力学模型的非饱和土抗剪强度预测方程。根据该模型,假设归一化水函数等于体积含水量。土体压缩至饱和时,吸力为零,接近孔隙,抗剪强度由饱和土体抗剪强度方程描述。这种方法在Aubeny和Lytton(2003)的设计指南中被重新使用。Lamborn(1986)模型的简化表达式为:
(10)众所周知的抗剪强度模型之一是Vanapalli等人(1996)提出的模型,其中饱和和剩余条件下的体积含水量必须从土壤-水特征曲线(SWCC)中估计。该模型的形式被其他几个与非饱和土壤数值模拟相关的研究使用或修改(Tarantino 2007;Alonso et al. 2010;Lu et al. 2010;Zhou et al. 2012;周生2015;拉什卡里和卡迪瓦尔2016;Kim et al. 2016)。
出发点是假设在较低的基质吸力值(或较高的饱和程度)下,孔隙水压力直接作用于增加有效应力,从而促进抗剪强度。这种情况一直适用,直到土壤在施加的基质吸力下开始去饱和。吸力对抗剪强度的贡献速率可以与归一化水面积有关。应用格林定理,水的归一化面积为:
(11)式中=剩余体积含水量,=饱和体积含水量,=匹配系数。为了简化,Vanapalli et al.(1996)在其扩展模型中假设。因此非饱和抗剪强度表示为:
(12)Fredlund et al.(1996)假设在特定应力状态下,基质吸力对非饱和土抗剪强度的贡献与归一化水域面积成正比。Garven和Vanapalli(2006)提出将归一化水域面积与土壤的塑性指数联系起来,其形式如下:
(13) (14)式中=塑性指数。
通过Bishop和Blight(1963)方程中的有效应力参数χ,将基体吸力归因于抗剪强度。然而,参数χ受到许多不同因素的影响,如干湿历史、加载路径、土壤类型和试样的内部土壤结构。?berg和S?llfors(1997)提出假设参数χ等于饱和度。一些研究人员在模拟非饱和土壤时也使用了类似的形式(Jommi 2000;Sheng et al. 2004;Gens等人,2006;Sun et al. 2007;Gallipoli et al. 2008;franois and Laloui 2008;Abed and Vermeer 2009;Burton et al. 2020;Shahrokhabadi et al. 2020)。该抗剪强度模型表达式为:
(15)式中=饱和度。
Khallili和Khabbaz(1998)通过施加一个经验常数来预测非饱和土的抗剪强度,扩展了Bishop的方程。根据收集的14个案例的数据集,所有土壤类型的基质吸力和空气入口值都响应于- 0.55的指数幂而减小。一些研究人员也通过研究非饱和土的本构行为回顾了这种形式(Khalili et al. 2004;Russell and Khalili 2006;Hamidi and Tourchi 2018)。抗剪强度模型为:
(16)式中AEV=空气入口值。
Tekinsoy等人(2004)提出了一种将基质吸力与抗剪强度联系起来的对数模型。其他几位作者也提出了类似形式的抗剪强度方程(Miao et al. 2002;Kayadelen et al. 2007;Satyanaga和Rahardjo 2019)。这种方法与以往的研究用进气量、基质吸力和大气压力之间的关系来描述土壤性质函数的方法相对不同。抗剪强度方程表示为:
(17)式中=大气压(101.325 Pa)。
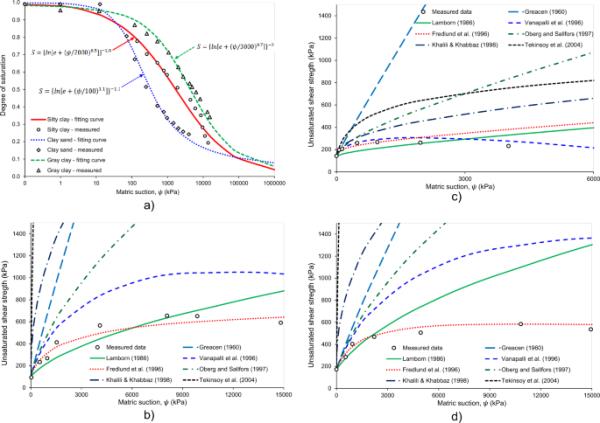
为了有效、可靠地验证抗剪强度模型,我们选取了30个已发表的数据集进行对比。对于一个实验数据集,测试了一些具有不同物理性质的土样。在本研究中,使用“case”一词来定义具有不同物理性质的样品,如不同的土壤类型、初始密度、塑性或饱和度。表1概述了实验数据集的基本特征。可以看出,几乎所有已发表的数据集都是针对四种主要的土壤类型进行的,即砂质、粘土、粉质和砂-高岭土。材料类型还包括天然土、膨胀土、尾矿和残余土。粘土含量为0 ~ 69.9%,土壤密度为松散~中密、致密。所有试验用例的基质吸力范围在0 ~ 1500kpa之间,饱和度范围在21.2% ~ 95%之间。此外,大多数土壤具有塑性指数PI,从0(砂土)到45(粘土)不等。因此,所选择的数据是完整的,可以认为是充分和可靠的,以评估抗剪强度模型的预测性能。此外,表2显示了使用理论模型计算抗剪强度所需输入参数的摘要。对分析计算参数的实际确定给予了特别注意。需要说明的是,进风值(AEV)和剩余体积含水量参数由土-水特征曲线确定,如图3所示。在之前的几项研究中也可以发现SWCC变量对非饱和抗剪强度的敏感性(Zhai et al. 2019;范教授2022 b;Pham and Sutman 2023b;Pham et al. 2023a, 2023b)。值得注意的是,SWCC和剪切试验是在不同围压下的不同土样上进行的。因此,在这两种类型的试验中,试样可能具有不同的初始孔隙比。为了更好地评价非饱和土的抗剪强度,采用基于剪切试验中土样真实孔隙比的标定swcc来计算非饱和土的抗剪强度。swcc的校准程序可以在Pham和Sutman (2022b)的论文中找到。
土壤-水特征曲线变量的确定
当前抗剪强度模型的有效性在本工作中是根据土样的基本物理特性来评估和分类的,其中含水量,空隙率和吸力经常被控制为恒定。工程师们会发现,基于初始物理性质的评估比考虑土壤样品的当前状态更有用和实用,土壤样品的含水量和空隙率随吸力的变化而变化。这是因为初始物理性质频繁且易于测量。最后,必须强调的是,目前的工作不允许我们评估考虑土壤体积变化的预测模型的性能。这主要是由于针对土体抗剪强度随体积变化的试验研究和现有模型数量有限。具体的测量结果和预测结果的比较见附录。
图4显示了使用Escario和Saez(1986)数据集的典型案例的预测和实测剪切强度-吸力曲线的比较。研究采用120 kPa压力下记录的土-水特征曲线(图5a)。表3为三种不同土型的土体性质及饱和抗剪强度参数汇总。实测抗剪强度用图中符号表示,连续线表示预测抗剪强度。值得注意的是,Vanapalli等人(1996)的模型在粘土砂的情况下与实验数据最吻合,而Fredlund等人(1996)的模型在粉质粘土和灰色粘土的抗剪强度的预测值和测量值之间产生了最吻合的结果。还发现Lamborn(1986)模型对低吸力范围产生了合理的预测。该比率是作为含水量的函数而涉及的,这是这些模型的共同特征。然而,其余基于与空气进入值的相关性的模型显示出严重的高估。
一个典型案例(Escario和Juca 1989年之后的试验数据)的预测抗剪强度与实测抗剪强度的比较:土-水特征曲线,b粉质粘土,c粘土砂,d灰色粘土
根据实测砂质土抗剪强度预测
图5比较了砂土的实测和预测抗剪强度。在低基质吸力范围内,抗剪强度模型的预测结果与实测数据非常接近,拟合良好。但随着基质吸力的增大,模型的预测结果开始出现明显的偏差。需要注意的是,各种抗剪强度模型的根本区别在于考虑了吸力对总抗剪强度的贡献。与净法向应力相比,低基质吸力对整体抗剪强度的贡献较小。这就解释了为什么在小的基质吸力下,预测模型之间的差异如此之小。当基质吸力由低到高增加时,所有抗剪强度模型的结果不一致。Tekinsoy等人(2004)对非饱和抗剪强度的预测过高,而Khalili和Khabbaz(1998)则严重低估了非饱和抗剪强度。与其他模型不同的是,其中两个模型是基于入风值定义土壤性质函数,而不考虑土壤饱和度。由Graecen(1960)模型定义的土壤性质函数也显示出由于使用体积空气含量而明显低估非饱和抗剪强度。
我们分析了五组粘土的数据,图6比较了预测的抗剪强度和实测的抗剪强度。研究结果表明,所选择的模型中没有一个产生的结果与所有比较案例中的测量数据一致。结果表明,对于所有不同的情况,所选择的模型都不能产生与实测数据一致的结果。几乎所有选择的模型都过高或过低地预测了非饱和土的抗剪强度。很明显,吸力和土壤密度的范围对各种模型的一致程度有实质性的影响。结果还表明,与其他模型相比,Greacen(1960)和Lamborn(1986)模型产生了最显著的过预测,而?berg和S?llfors(1997)和Tekinsoy等(2004)模型在所有情况下产生了最显著的过预测。相反,在所选择的所有模型中,Fredlund等人(1996)的模型通常与测量数据的一致性最好。此外,还发现当基质吸力增大时,预测结果与实测结果的差异也增大。
根据实测的粘土抗剪强度进行预测
图7显示了粉质土的预测抗剪强度与实测抗剪强度的对比。结果表明,所选模型与实测数据均不一致。Fredlund等人(1996)和Vanapalli等人(1996)开发的模型与测量结果有很好的一致性,总体上优于其他抗剪强度模型。即使在低基质吸力范围内,Graecen(1960)、Lamborn(1986)和Khalili和Khabbaz(1998)的模型也大大低估了非饱和抗剪强度。因此,这些模型对于粉质土的抗剪强度估计是不够的。与测量结果相比,Tekinsoy等人(2004)的模型严重高估,而?berg和S?llfors(1997)的模型略微高估。
根据测量的粉质土抗剪强度进行预测
图8给出了砂-高岭土混合物的预测抗剪强度与实测抗剪强度的对比。可以看出,模型的预测潜力在很大程度上取决于吸力范围和土壤的物理性质。总的来说,对于大于100kpa的抗剪强度范围,所选模型与实测数据的拟合度均不理想。一般来说,Tekinsoy等人(2004)和Khalili和Khabbaz(1998)的模型产生了高估,而其余模型通常产生了低估。值得注意的是,?berg和S?llfors(1997)模型经常预测的结果低于实测抗剪强度。假设土性函数中的分量等于饱和程度,有可能显著低估砂-高岭土混合物的抗剪强度。
根据实测砂-高岭土混合料的抗剪强度进行预测
众所周知,抗剪强度与基质吸力之间的关系往往遵循一条非线性曲线。曲线拟合程度的判据是指实测结果与预测结果的收敛程度,用来评价分析模型的性能。预测曲线与实测曲线之间的差值较低,表明用方程更好地描述了数据。曲线的匹配程度用一个指标来表示,即平均相对误差(ARE)。由下式可知,平均相对误差是实测值与预测值之差的比例:
(18)其中,τmeasured为第i个数据的实测抗剪强度值,τpredict为第i个数据的预测抗剪强度,N为可用数据点总数。
标准化的平方误差和(SSE)用于衡量抗剪强度模型预测结果的程度,作为第二个标准。如果归一化后的误差平方和较低,说明分析模型的使用更可靠。误差平方和的定义如下:
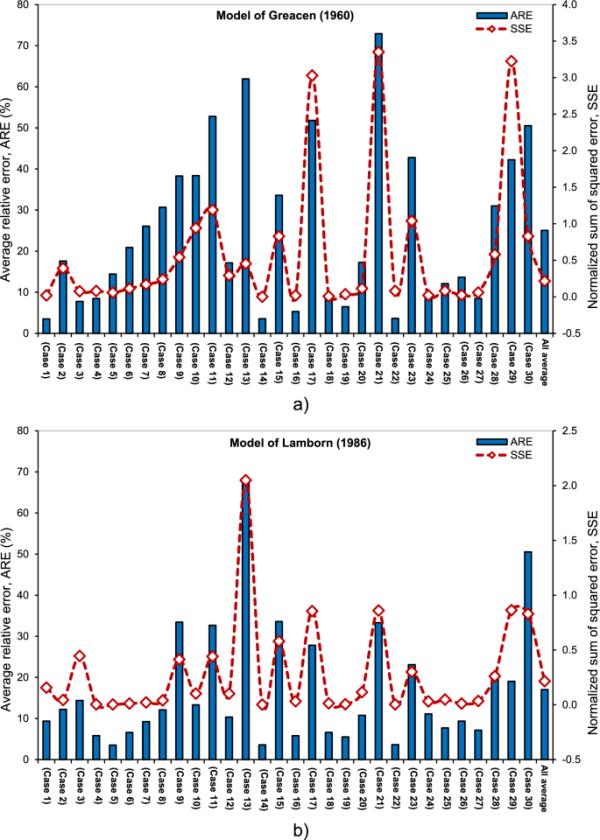
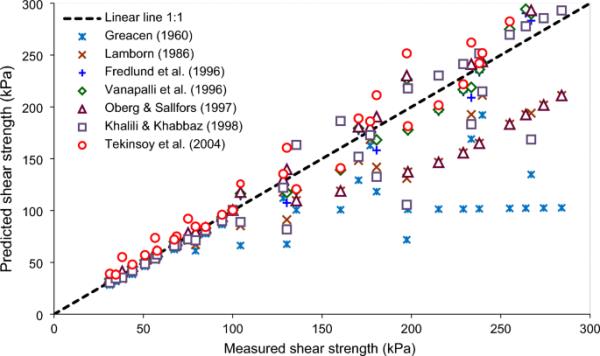
(19)在统计分析方法中描述了两个关键因素,即预测结果的质量和一致性,这为理论模型预测结果的能力提供了一个广泛的视角。对于所有30个测试案例中所选择的抗剪强度模型,图9显示了归一化的平方误差和平均相对误差。ARE和SSE分布的大范围突出了这样一个事实,即在所有可能的情况下,没有一个分析模型提供与测量数据一致的协议。控制非饱和土行为的机制背后的复杂性可能是这种不一致的原因。结果表明,Fredlund et al.(1996)模型的总体平均相对误差为12.1%,Vanapalli et al.(1996)模型为13.75%,?berg和S?llfors(1997)模型为15.3%,Lamborn(1986)模型为17.1%,Khalili和Khabbaz(1998)模型为16.8%,Greacen(1960)模型为25.7%,Tekinsoy等(2004)模型为29.2%。Fredlund et al.(1996)、Vanapalli et al.(1996)、?berg和S?llfors(1997)开发的三种抗剪强度模型在预测方面明显优于其他模型。这些结果还强调了一个模型的预测能力在多大程度上取决于土壤的物理特性和吸力范围。

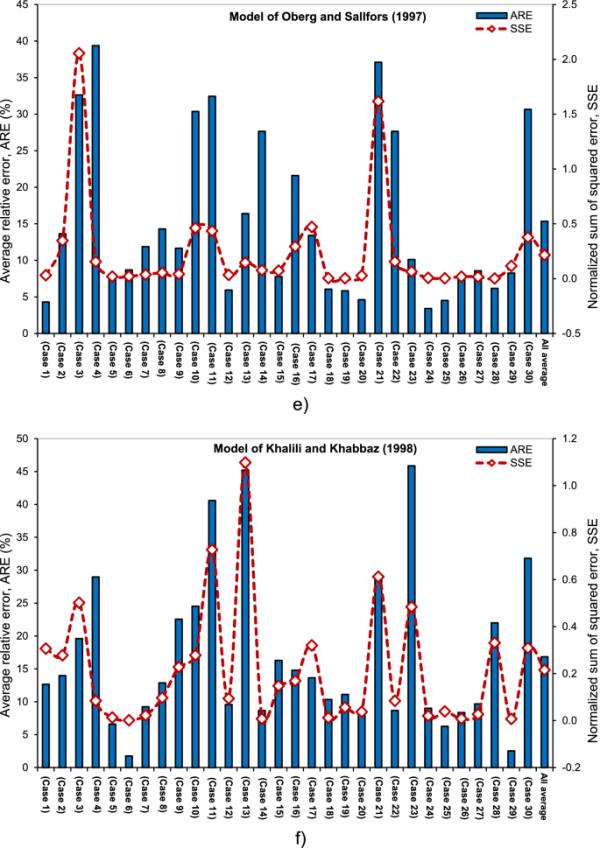

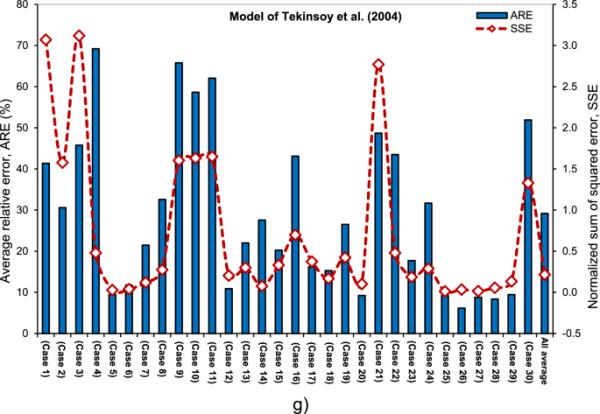
七种抗剪强度模型的统计分析:Graecen(1960)模型b模型Lamborn (1986), c模型Fredlund et al. (1996);Vanapalli et al.(1996)的d模型;e模型?berg和S?llfors (1997), f模型Khalili和Khabbaz (1998);Tekinsoy等人(2004)的g模型
四种主要的土壤类型(沙质、粘土、粉质和砂高岭土)在公布的数据集中进行了测试,如前面部分所述。应该强调的是,每种类型的土壤在固相和液相之间似乎都有一种独特的复杂的相互作用。因此,对各种土壤类型的抗剪强度模型性能进行分类并确定每种土壤类型的最佳模型至关重要。
图10显示了所选抗剪强度模型下四种不同土壤组的平均相对误差(ARE)。可以看出,砂土的ARE值明显低于其他土类型,说明分析模型在预测砂土抗剪强度方面优于粘土土。需要指出的是,粘性土由于其在形状、大小、结构排列和水分分布现象等方面的特点,往往表现出比颗粒土更复杂的行为。此外,砂土的吸力范围远低于粘土,这使得模型可以更准确地预测抗剪强度。Fredlund等人(1996)和?berg和S?llfors(1997)的模型被证明是预测砂土非饱和抗剪强度的两种最有效的选择。需要注意的是,砂质土的塑性指数往往较小,参数κ (Eq. 14)接近于1.0。因此,?berg和S?llfors(1997)模型与Fredlund et al.(1996)模型变得相似,这就解释了为什么两种模型对沙质土壤的平均相对误差如此接近。结果表明,Bishop参数χ=饱和度的假设对砂土较为适用,对粘土则不合理。Vanapalli et al.(1996)开发的模型总体上优于所有其他粘土模型,可以认为是预测非饱和抗剪强度的最佳选择。而Vanapalli et al.(1996)提出的剩余体积含水量对土壤结构变化和体积应变比较敏感。该模型对粉质土非饱和抗剪强度的预测精度高于砂-高岭土混合土的非饱和抗剪强度。沙子-高岭土混合物在取样过程中被压实,从而产生高密度和更大的基质吸力范围。来自?berg和S?llfors(1997)、Vanapalli等人(1996)和Fredlund等人(1996)的三个模型也被发现是估计粉质土壤和砂-高岭土混合物抗剪强度的可靠候选模型。此外,值得注意的是,与使用含水量的模型相比,使用空气进入值或空气体积含水量来关联吸力和抗剪强度的模型(Greacen, Khalili和Khabbaz, Tekinsoy等人)的预测能力较差。
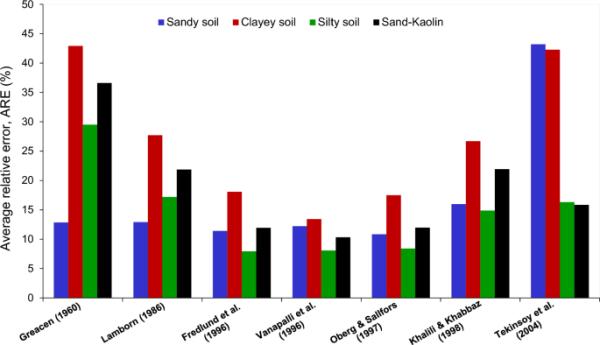
基于土体类型的抗剪强度模型性能
图11显示了粗粒度(砂土)和细粒度(粘土)土壤的微观结构差异,以演示不同的土壤类型如何影响预测模型的性能。值得注意的是,粘土颗粒通常呈板状,而砂粒通常呈近球形。许多早期的研究指出,粘土的形成是复杂的,更多的颗粒重新定向平行于另一个,而不是滚动,因为它发生在砂结构中,基于显微照片的发现(Dhadse et al. 2023)。此外,压实粘土的微观结构表现出双重孔隙网络,具有两个相互作用水平:微观结构水平对应于活性粘土矿物及其附近(团聚体内空隙),主要是物理化学相互作用现象,宏观结构水平说明土壤的更大尺度结构(团聚体间空隙)(Wan et al. 1995;Romero et al. 1999;罗哈斯2008;Airò Farulla et al. 2010;Eyo et al. 2019)。由于高电荷粒子对水的吸引和毛细作用,较小的团聚体内部空隙会在团聚体间空隙之前达到水饱和。这表明在压实粘土中,基质吸力、含水量和团粒内土体结构之间存在定性关系。因此,除了整体含水量外,集料内空隙的局部含水量也会影响基质吸力对抗剪强度的贡献水平。因此,基质吸力对抗剪强度的贡献不仅取决于土体的整体含水量,还取决于集粒内空隙的局部含水量。然而,大多数的抗剪强度方程往往是使用简单的回归技术来建立实验数据,而忽略了潜在的物理原理。因此,粘土的预测模型性能远低于砂土的预测模型。
细观结构和毛细力示意图:砂团;b粘土簇,c砂粒间的半月板,d粘土粒间的半月板
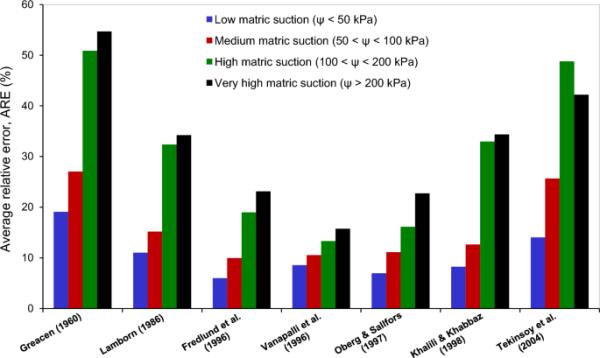
基质吸力的大小对抗剪强度模型预测结果的差异有很大影响。因此,有必要基于基质吸力范围来评价抗剪强度模型的性能。本节中,“低水平”定义为基质吸力小于等于50kpa,“中等水平”定义为基质吸力在50 ~ 100kpa之间,“高水平”定义为基质吸力在100 ~ 200kpa之间,“非常高”定义为基质吸力大于200kpa。
所选择的抗剪强度模型在不同基质吸力范围内的对比如图12所示。值得注意的是,在低值范围内,与净法向应力分量相比,基质吸力对总抗剪强度的贡献很小。因此,抗剪强度模型对低基质吸力条件下非饱和抗剪强度的预测效果较好(平均相对误差小于10%)。模型的预测性能随基质吸力的增大而变化,总体上呈下降趋势。Fredlund et al.(1996)、?berg和S?llfors(1997)模型对吸力小于100 kPa的非饱和土抗剪强度的预测效果最好。然而,Vanapalli等人(1996)的模型给出了最低的平均相对误差,这在预测较高基质吸力(> 100 kPa)范围内的抗剪强度方面产生了最好的性能。结果表明,Bishop参数χ等于饱和度的假设更适用于低基质吸力,而不适用于高基质吸力。随着基质吸力的增大,气相与水相之间的相互作用变得更加复杂,有效饱和度可以更充分地描述土体抗剪强度与吸力的关系。此外,所有其他剩余模型(Greacen, Lamborn, Khalili和Khabbaz, Tekinsoy等人)的预测性能都很低,特别是对于高基质吸力。

基于基质吸力范围的抗剪强度模型性能
边界效应状态、过渡状态和残余状态被确定为三个可区分的去饱和阶段。图13显示了不同基质吸力状态下水的分布情况。当存在边界效应或吸力较低时,水几乎填满了所有的土壤孔隙,在团聚体或土壤颗粒之间形成水半月板。过渡态吸力增大,含水率明显降低。因此,与土壤或团聚体接触的水半月板面积不是连续的,并在此阶段开始减少。吸力的大幅增加最终导致含水量相对较小的变化,并且在水半月板很少明显的残余阶段。应注意的是,最大的非线性抗剪强度增加发生在过渡区。在剩余吸力条件下,非饱和土的抗剪强度在进一步的去饱和过程中会增加、减少或保持近似不变。在某些情况下,抗剪强度可能会降低,特别是在快速饱和的土壤中(如沙子和淤泥)。实际上,在残余吸力条件下,砂土和粉土中的含水量可能很低,这可能使吸力难以适当地传递到土壤颗粒或团聚体的接触点。因此,即使吸力大大增加,抗剪强度也不太可能显著提高。另一方面,粘土可能没有明确定义的残余状态,因为它的聚集体内部空隙中充满了许多层吸附的水。当施加的吸力较低时,大部分集料间空隙和全部集料内空隙保持饱和状态。吸力增大时,只有微观结构保持饱和状态,有利于抗剪强度的提高。因此,如果在建模时考虑不同脱饱和阶段的含水率变化,预测将更加准确。与其他模型相比,Vanapalli et al.(1996)模型利用与剩余水含量直接相关的有效饱和度对高吸力范围具有更好的预测性能。其他忽略残余阶段机理的模型对高吸力范围的预测不成功。

不同阶段吸水面积随吸力的变化
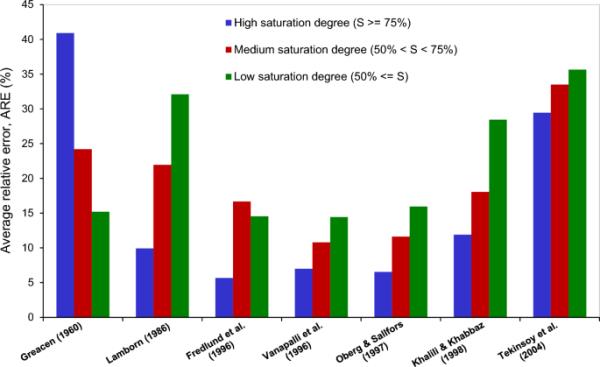
必须认识到非饱和土的抗剪强度受基质吸力和饱和度两个单独因素的控制。饱和程度经常包含在用于表征基质吸力对抗剪强度贡献的土性质函数中。不同抗剪强度模型对饱和程度的影响也不同。因此,评估现有的抗剪强度模型在不同饱和度范围内的表现是至关重要的。饱和度分为低饱和度(50%)、中饱和度(50% < 75%)、高饱和度(75% < 100%)三个级别。
图14显示了理论模型在不同饱和度范围内的有效性。研究结果表明,随着饱和度的增加,各模型的性能都有所下降。但与基质吸力模型相比,饱和度模型的灵敏度较小。需要强调的是,Khalili和Khabbaz(1998)以及Tekinsoy等人(2004)的模型在各种饱和度范围内的预测性能都很差。土壤性质函数使用Khalili和Khabbaz(1998)和Tekinsoy等人(2004)的模型定义,基于空气进入值而不考虑饱和程度。这就解释了为什么这些模型在任何饱和度范围内都会产生很大的分歧。其余模型对饱和度大于50%时非饱和土抗剪强度的预测效果较好。在Graecen(1960)的模型中,使用体积空气含量来定义土壤性质函数。当饱和度小于50%时,体积空气含量近似于体积水含量。这就解释了为什么Greacen(1960)的模型能很好地预测低饱和度。当饱和度大于50%时,Vanapalli et al.(1996)、?berg和S?llfors(1997)模型的预测性能优于其他模型。在所有选择的候选模型中,Vanapalli et al.(1996)、Fredlund et al.(1996)、?berg和S?llfors(1997)三个模型在预测不同饱和度范围内非饱和土的抗剪强度方面给出了最好的结果。
基于饱和度范围的抗剪强度模型性能
对于饱和度的低值范围,可以看出目前几乎所有的模型在预测方面都表现不佳。因此,为了正确理解这些模型的局限性,必须考虑孔隙水对非饱和土力学行为的贡献。典型非饱和土截面上土单元表面和内部应力分量的平衡如图15所示。研究发现,非饱和土的整个横截面积是由饱和部分面积和非饱和部分面积结合得到的。非饱和土孔隙水可分为体积水、毛细水和吸附水三种类型。孔隙水的表达式为:
(20)式中,S=总饱和度,,=散装水、毛细水和吸附水的组分。

非饱和土截面的应力平衡
应该强调的是,通过土骨架从一个边界表面转移到另一个边界表面的接触应力分量直接负责平衡部分施加荷载,其余部分由孔隙水压力承担。散装水在土壤颗粒之间包含一些接触点,并且它可以在土壤骨架旁边支持外部负载,以及(Karube和Kawai 2001)。此外,土颗粒之间存在毛细水,毛细水的压力影响土颗粒之间的接触应力,影响抗剪强度。然而,吸附水对土壤抗剪强度的贡献很小(Konrad and Lebeau 2015)。原则上,这是因为每个土壤颗粒的表面都完全被吸附的水覆盖,这对土壤颗粒之间的接触应力几乎没有影响。在这种情况下,正确的有效应力应改写为体积和毛细水的函数:
(21)然而,在本研究中所考虑的抗剪强度模型中,没有一个能够区分散装水和毛细水对非饱和土抗剪强度的贡献。因此,几乎所有的模型都典型地高估了结果,特别是在低饱和度的情况下,吸收的水的影响更为明显。
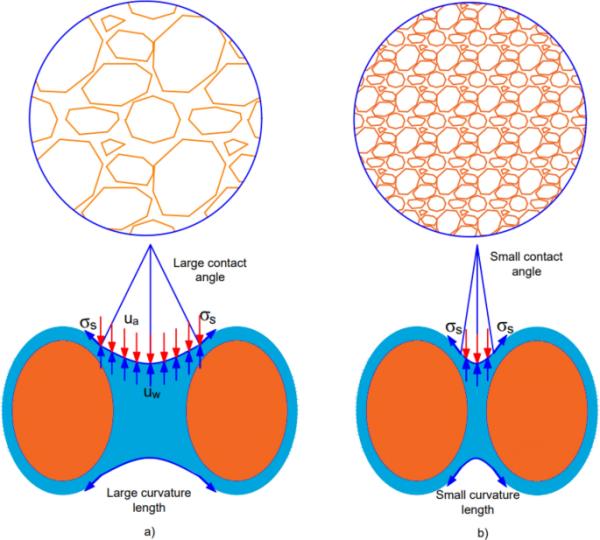
非饱和土的抗剪强度不仅与含水量有关,而且与土的密度有关。这是因为孔隙大小对水、空气和固相的相互作用有重要影响(Bencheikh和Messast 2023)。根据最近的非饱和土力学理论,土壤元素通常被视为由孔隙空气、孔隙水和固体颗粒组成的简单三相系统。空气-水半月板的曲率与引起吸力的毛细作用有关,这归因于空气-水半月板之间的相互作用:
(22)式中=孔隙半径,=表面张力,=气水接触角,=气水半月板曲率长度。
总吸力对空隙比的微分可表示为:
(23)土壤密度已被观察到类似于固体颗粒的排列。因此,土壤密度的任何变化都会导致饱和度和体积含水量的变化。密度的变化也会影响土壤颗粒的堆积程度,这将影响接触角、空气-水半月板的曲率,从而影响土壤中的基质吸力(图16)。
土壤密度对空气-水半月板曲率的影响
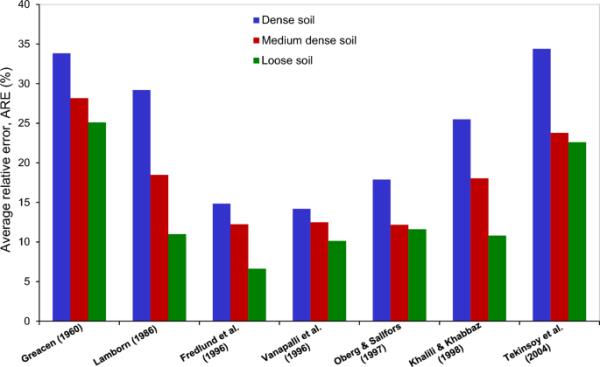
为了了解抗剪强度模型对孔隙大小变化的反应,有必要根据土壤密度对性能进行分类。分析模型的平均相对误差随初始土壤密度变化如图17所示。随着土壤密度的增加,模型的预测精度下降。所选的抗剪强度模型的结果与致密土的实测结果都不太一致。没有一个抗剪强度模型被用来产生与致密土的测量数据一致的结果。所有的抗剪强度模型对致密土的平均相对误差都在15%以上。致密土具有复杂的相互作用性质,伴随着孔隙大小和水分分布现象,这可以解释致密土的ARE值明显高于疏松土的原因。此外,需要注意的是,密度越高的土壤孔隙尺寸越小,因此其基质吸力会变得非常高。结果表明,随着土体密度的增大,抗剪强度模型的预测精度下降。此外,还发现土密度对理论模型预测能力的影响比基质吸力和饱和度的影响更为显著。遗憾的是,现有的抗剪强度模型都忽略了土密度的影响。不幸的是,目前使用的抗剪强度模型都没有考虑土壤密度。可以看出,Vanapalli et al.(1996)的模型在预测致密土抗剪强度方面表现最好,而Fredlund et al.(1996)的模型在预测松散土抗剪强度方面表现最好。此外,在整个土壤密度范围内,Vanapalli等人(1996)、Fredlund等人(1996)、?berg和S?llfors(1997)的三个模型在预测性能方面往往优于其他模型。
基于土密度的抗剪强度模型性能
土壤越细,塑性指数(PI)通常越大,它衡量的是土壤具有塑性的含水量范围。然而,众所周知,土壤含水量的变化往往会导致土壤抗剪强度的变化。塑性指数考虑了改变土壤含水量对其强度和压缩性的影响。在颗粒土中,含水量的变化对这些特性的影响有限,而黏性土往往随着含水量的减少而变得明显更强,可压缩性更低。因此,在评估理论模型的敏感性和对其性能进行分类时,塑性指数可能是一个重要的考虑因素。根据塑性指数将土壤的塑性分为低塑性(10)、中塑性(20)和高塑性(20)三类。
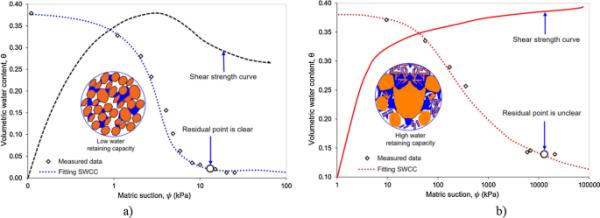
毛细管内聚力是一种复杂的物理系统,是土壤颗粒和水分子之间相互吸引的结果。因此,水分含量是迄今为止影响土壤黏性的最明显因素。当土壤含水量低于塑性极限(低塑性指数)时,土壤变得干燥松散,土壤颗粒相互接触形成环状水膜,但不足以形成网络。因此,对于塑性较低的土体,基质吸力对抗剪强度的影响最小。当残余阶段基质吸力增大时,此时的抗剪强度曲线有减小的趋势(图18a)。
土的塑性和抗剪强度:a低塑性,b高塑性
对于塑性较高的土体,土体空隙之间的水膜足够连接形成网络,增加了土体的黏聚力。这是由于粘土颗粒的显著比表面积以及团粒内空隙的存在。因此,对于塑性较高的土体,基质吸力对抗剪强度的影响更为显著。在这种情况下,在残余阶段,随着基质吸力的提高,抗剪强度曲线趋于增大或大致保持不变(图18b)。
抗剪强度模型在三种不同土壤塑性水平下的有效性如图19所示。研究结果表明,对于中塑性土壤,所有的分析模型都表现不佳,其中Vanapalli et al.(1996)的预测性能最好,ARE约为15%。另一方面,Fredlund et al.(1996)开发的模型在高塑性土壤中表现出最好的结果。除了Graecen(1960)和Tekinsoy等人(2004)的模型外,低塑性土壤的分析模型的性能非常相似。此外,Graecen(1960)、Lamborn(1986)、Khalili和Khabbaz(1998)的模型对土壤可塑性的敏感性明显高于Fredlund等人(1996)、Vanapalli等人(1996)、?berg和S?llfors(1997)等采用归一化含水量的模型。还应强调的是,高塑性土壤产生更高的基质吸力,因此理论模型的预测性能通常会降低。
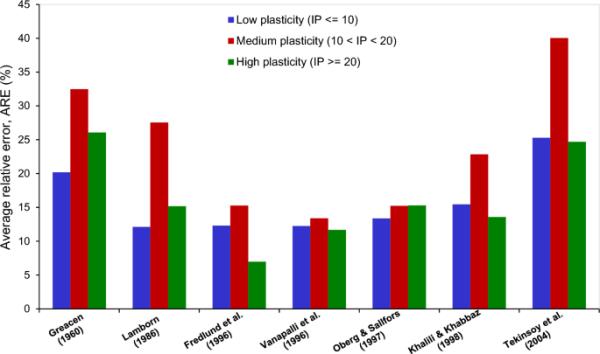
基于塑性指标的抗剪强度模型性能研究
同样值得注意的是,非饱和抗剪强度受到土颗粒周围毛细作用的显著影响。非饱和土的抗拉强度受颗粒间相互作用和颗粒区水分分布的影响,而颗粒区水分分布因不同粘土矿物的存在而发生显著变化。因此,建立黏土活性与抗剪强度模型有效性之间的联系可能是有利的。利用粘土颗粒在土壤中所占百分比的塑性指数来计算粘土活度(),从而识别粘土的膨胀潜力。在本研究中,将土壤分为低活性或无活性(0.5)、中等活性或正常(1.0)和高活性或有活性(1.0)三个不同水平的粘土活性。
值得一提的是,基质吸力的大小和孔隙水量决定了基质吸力对非饱和土抗剪强度的贡献程度。同时提高基质吸力和含水率时,抗剪强度增大到最大值。然而,在基质吸力和含水量之间存在反比函数。因此,总有一个最佳的含水量比,使非饱和土具有最高的抗剪强度,而这个比例在很大程度上取决于细土含量的存在。图20描述了土壤微观结构与三个活动级别的关系。需要注意的是,低活度对应于低塑性指数和高粘土含量的情况,而高活度对应于高塑性指数和低粘土含量的情况。然而,较高的粘土含量也表明更大的持水能力,因此塑性指数可能更大。随着细粒土用量的增加,砂粒之间的有效接触增加,吸附力增大。从上面的分析可以看出,在非饱和土中加入有限数量的粘土也会导致非常复杂的行为。

活性、含水量和粘土含量之间的相关性为:a低活性,b中等活性,c高活性
图21显示了粘土活性变化时抗剪强度模型的预测性能。重要的是要注意,特别是对于中等和高活性土壤,没有一个分析模型产生的结果与测量值很好地一致。对于每一个粘土活度水平,各抗剪强度模型的平均相对误差往往大于10%。Vanapalli等人(1996)模型的ARE值值得注意,因为它对于所有三个活动水平大致相同,从而得出活动对模型性能的影响较小的结论。造成这种趋势的一个重要原因是,Vanapalli等人(1996)的模型在预测中考虑了剩余饱和度,从而将粘土活性的影响降至最低。在所选择的模型中,Fredlund et al.(1996)模型对低活性和中等活性土壤的预测性能最好。至于其余的模型,更有趣的是强调预测模型的准确性通常会随着粘土活性的增加而下降。粘土活性的差异对几种模型有相当大的影响,其中最著名的是Graecen(1960)和Lamborn(1986)的模型。使用体积含水量将非饱和抗剪强度与吸力联系起来,而该参数在很大程度上取决于土壤中的粘土含量,可以认为是这种敏感性的原因。
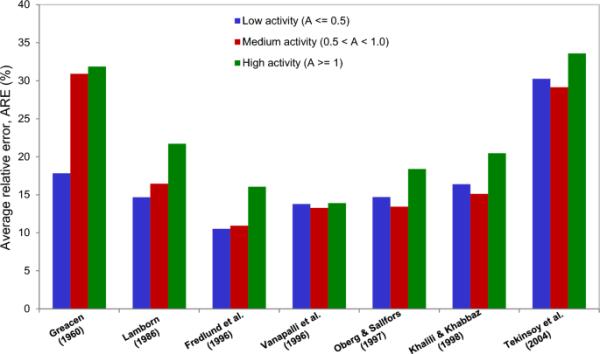
基于粘土活性的抗剪强度模型性能
为了提供一个基准,设计工程师可以使用统计摘要来确定哪些模型适合各种土壤条件。使用平均信息准则(Pham and Sutman 2022a)评估每个模型的性能;范教授2020 b;Pham and Dias 2021)。表4概述了每个模型在不同土壤条件下的表现。对于每个相关参数使用的最佳模型将是具有最低ARE的模型。预测非饱和抗剪强度所选择的模型,一般应小于20%,在可接受的范围内。
发表评论
暂时没有评论,来抢沙发吧~